Anomalieerkennung in Zeitreihen: Welcher Algorithmus ist der Richtige?

In einem vorherigen Beitrag wurden die Bedeutung und der Umgang mit Anomalien im Industriekontext beleuchtet. Die Identifizierung und der richtige Umgang mit Anomalien haben branchenübergreifend eine große Bedeutung und sind die Basis für ein bis dato nicht mögliches vorausschauendes, wirtschaftliches Handeln.

Entscheidend dabei ist die Wahl des richtigen Algorithmus. Dabei hängt diese Wahl nicht nur davon ab, welche Arten von Anomalien erkannt werden sollen, sondern auch von der Datenstruktur selbst.

Die Arten von Anomalien

Grundsätzlich kann man zwischen zwei Arten von Anomalien unterscheiden: Univariate Anomalien beschreiben Ausreißer innerhalb einer Stichprobe von Werten (bspw. Sensormesswerte einer Maschine).

Multivariate Anomalien sind hingegen ungewöhnliche Messungen in mehreren Variablen. In beiden Fällen gibt es verschiedene Ansätze, um Ausreißer zu erkennen und zu bereinigen. In diesem Beitrag werden wir uns mit der Anomalieerkennung in (zeitlich) geordneten, eindimensionalen Daten –Zeitreihen – beschäftigen.

Weiterhin können Anomalien entweder lokal oder global sein. Eine globale Anomalie ist ein ungewöhnlicher Datenpunkt für die gesamte Datengrundlage. Eine lokale Anomalie ist im Hinblick auf die gesamte Datenmenge nicht zwangsläufig ungewöhnlich, aber durchaus im Kontext, in dem der Datenpunkt aufgetreten ist. So ist eine Temperaturmessung von 18° C im gesamten Jahresverlauf nicht ungewöhnlich. Wird der Wert jedoch im Winter gemessen, würde man ihn als lokale Anomalie einstufen.

Anomalien im Zeitverlauf erkennen – mehr als einfache Grenzwerte

Bevor man über die Erkennung – geschweige denn Bereinigung – von Anomalien nachdenkt, ist die erste Frage, die es zu beantworten gilt: Wann ist ein Datenpunkt eine Anomalie? Eine intuitive und simple Lösung dieser Frage ist die Festlegung von Grenzwerten, die auf Erfahrung oder Expertenwissen basieren. Liegt ein Datenpunkt außerhalb der definierten Grenzen, wird er als Ausreißer eingestuft. Vor allem für univariate Zeitreihen -beispielsweise Sensordaten- ist dieses Vorgehen weit verbreitet, um anomales Verhalten zu detektieren. Dieses Verfahren der Anomalieerkennung hat aber deutliche Nachteile. Entscheidend ist, dass die Grenzwerte über einen längeren Zeitraum statisch sind und somit Strukturveränderungen im Zeitverlauf nicht berücksichtigen. Die Grenzwerte dienen also lediglich zur Erkennung globaler Anomalien, also Werten die grundsätzlich ein ungewöhnliches Maschinenverhalten suggerieren. Ändert sich das Niveau der Messwerte (z.B. durch eine höhere Auslastung der Maschine), müssen auch die Grenzwerte angepasst werden, da sich das „normale“ Verhalten der Messwerte verändert hat. Für einen solchen Anwendungsfall wird also ein Kriterium benötigt, dass die derzeitige Struktur der Zeitreihe berücksichtigt, um lokale Anomalien zu finden.

Wie arbeiten die Algorithmen?

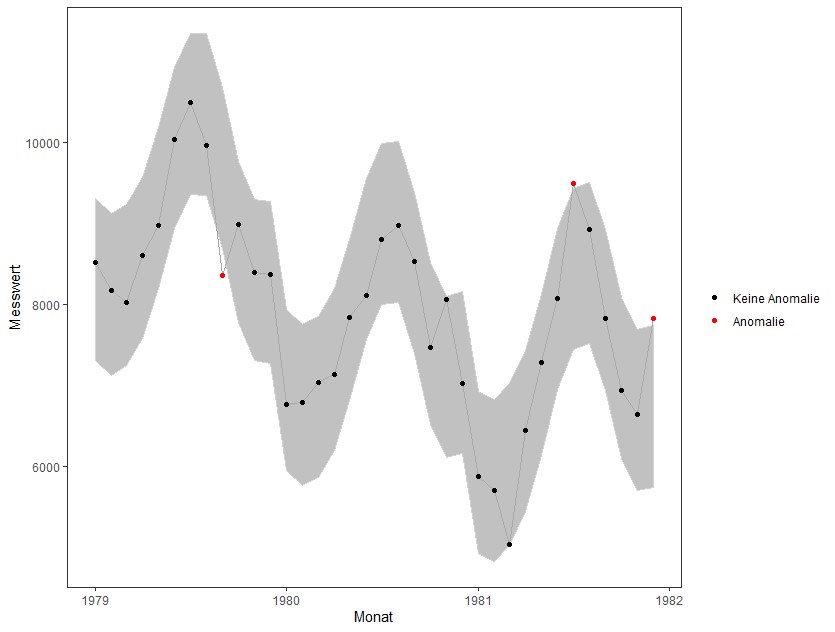
Viele Algorithmen, die zur Erkennung von Anomalien verwendet werden, versuchen daher zunächst eine Trend- und eine Saisonkomponente in der Zeitreihe zu erkennen und diese aus der Zeitreihe zu entfernen. Das ermittelte Trend- und saisonale Verhalten kann für den jeweiligen Zeitraum als normales Verhalten der Zeitreihe interpretiert werden. Interessant ist dabei die Abweichung die zwischen den tatsächlich gemessenen Werten und den im Hinblick auf Trend und Saisonalität zu erwartenden Werten. Ist die Abweichung zu groß, liegt wahrscheinlich eine Anomalie vor. Die Annahme dabei ist, dass die verbleibende Restkomponente standardnormalverteilt ist. Es ist also zu erwarten, dass zwar im Mittel keine Abweichung von Trend und Saisonalität vorliegen, Abweichungen aber grundsätzlich nicht ungewöhnlich sind. Je größer die Abweichungen jedoch werden, desto wahrscheinlicher ist es, dass ein Ausreißer vorliegt. Davon ausgehend basieren viele Verfahren zur Anomalieerkennung auf dem Ausreißertest des amerikanischen Statistikers Frank Grubbs, der für die Erkennung von Ausreißern in normalverteilten Stichproben (in diesem Fall der Restkomponente einer Zeitreihe) konzipiert ist. Die Algorithmen, die diesem Ansatz folgen, unterscheiden sich untereinander vor allem in der Bestimmung der Restkomponente. Dabei sind die jeweiligen Algorithmen auf eine bestimmte Struktur in den vorliegenden Daten ausgelegt. Überwiegt der saisonale Einfluss in der Zeitreihe, genügt die Annahme, dass der Trend durch den Median abgebildet wird. Liegt eine einflussreiche und langfristige Trendkomponente vor, werden häufig Methoden wie LOESS (Locally Estimated Scatterplot Smoothing; eine Erweiterung einer klassischen Kleinste-Quadrate-Regression) benutzt, um die Trendkomponente der Zeitreihe und somit die Restkomponente zu bestimmten.

 

Einsatz von Clusteralgorithmen

Ein weiterer Ansatz ist die Nutzung von Clusteralgorithmen, um die Punkte der Zeitreihe in sinnvolle Gruppen zu unterteilen. Herkömmliche Algorithmen setzen hierfür eine feste Anzahl an Clusterzentren voraus und versuchen eine entsprechende Anzahl an Gruppen zu bilden, sodass die Punkte so nah wie möglich an ihrem zugehörigen Clusterzentrum liegen (z.B. k-Means). Algorithmen wie Dbscan (Density Based Spatial Clustering of Applitcations with Noise) definieren für jeden Punkt eine Nachbarschaft, die aus allen Punkten besteht, die um höchstens einen vorher festgelegten Abstand zum Punkt entfernt sind. Auf diese Weise entstehen drei Arten von Punkten: Kernpunkte, Randpunkte und Ausreißer. Kernpunkte zeichnen sich dadurch aus, dass sie eine Mindestanzahl von Punkten in ihrer Nachbarschaft aufweisen. Randpunkte weisen zwar nicht genügend Punkte in ihrer Nachbarschaft auf, sind jedoch von einem Kernpunkt erreichbar. Eine Menge von Kernpunkten, die untereinander erreichbar sind und alle zugehörigen Randpunkte bilden ein Cluster. Ausreißer sind somit Punkte, die nicht von einem Kernpunkt erreichbar sind, geschweige denn genügend Punkte in ihrer Nachbarschaft aufweisen und somit keinem Cluster zugewiesen werden können. Solche Clusteralgorithmen sind sehr robust gegenüber Strukturveränderungen (bspw. eine zeitweilig höhere Maschinenauslastung), vernachlässigen jedoch die zeitliche Struktur der Daten. Somit werden zum Beispiel saisonale Strukturen nicht berücksichtigt, da das Clustering über Punkte in der Nachbarschaft nicht vorherige Perioden in Betracht zieht. Davon abgesehen bieten Clusteralgorithmen jedoch ebenfalls eine effiziente und nachvollziehbare Möglichkeit, um Ausreißer zu erkennen.

—

Sie wollen mit der Anomalieerkennung die Verfügbarkeit Ihrer Systeme und Anlagen erhöhen?  Sprechen Sie uns an.