Warum KI erklärbar sein sollte

Haben Sie sich gefragt, wodurch ersichtlich wird, dass eine Ihrer Maschinen zeitnah ausfallen wird? Woran können Sie erkennen, ob Ihr Kunde eine Versicherung bei Ihnen abschließen wird? Weshalb wurde Ihre getätigte Transkation als anormal klassifiziert und dadurch ihre Kreditkarte gesperrt? Fanden Sie sich schon einmal in einer der erwähnten Situationen wieder oder haben Sie vielleicht eine ähnliche Gegebenheit erlebt?

Würden Sie gerne wissen, wieso das Ergebnis so aussah wie es aussah? Das ist völlig normal. Insbesondere, wenn diese Entscheidung nicht von einem anderen Menschen selbst sondern von einem Algorithmus getroffen wurde, ist eine Begründung für die Entscheidung besonders wichtig.

SHAP: Eine besondere Methode im Fokus

In diesem Beitrag wollen wir tiefer in die Welt der XAI eintauchen. Genauer gesagt wollen wir eine bestimmte Methodik näher beleuchten, und zwar SHAP (SHapley Additive exPlanation). SHAP kann domänenunabhängig eingesetzt werden und liefert visuell ansprechende Grafiken für Business-Anwender. Mit der Relevanz und den möglichen Auswirkungen der Nutzung von XAI haben wir uns bereits in einem vergangenen Blogartikel beschäftigt.

SHAP ist vermutlich der bekannteste Ansatz aus der Welt der XAI. Hierbei handelt es sich im Allgemeinen um eine sogenannte modell-agnostische XAI-Methode. Model-agnostisch bedeutet, dass SHAP in der Lage ist, die Entscheidungen von prinzipiell jedem Machine Learning-Modell erklären zu können. Zudem kann SHAP mit verschiedenen Datenformaten umgehen, wie z.B. Bild-, Text- oder tabellarische Daten. Die Flexibilität, SHAP in diversen Problemstellungen anzuwenden, ist ein großer Vorteil dieser Methodik.

SHAP basiert auf den Shapley-Werten aus der Spieltheorie. Hierbei wird verglichen, wie sich das Modell verhält, wenn ein bestimmtes Feature in einer Featureauswahl enthalten ist oder nicht. Features, die in einer Featureauswahl nicht enthalten sind, werden durch zufällig bestimmte Werte aus dem Hintergrunddatensatz aufgefüllt. Dieser Vorgang wird je Feature im Datensatz für alle möglichen Featurekombinationen wiederholt. Schließlich wird ein gewichteter Mittelwert von allen möglichen Kombinationen gezogen. Dieser nun errechnete Wert ist der Shapley-Wert dieses speziellen Features. Je höher der Betrag des Shapley-Werts ist, umso größer ist der Einfluss der Variable auf die Prädiktion. Werte um Null spiegeln somit nur einen geringen Einfluss wider.

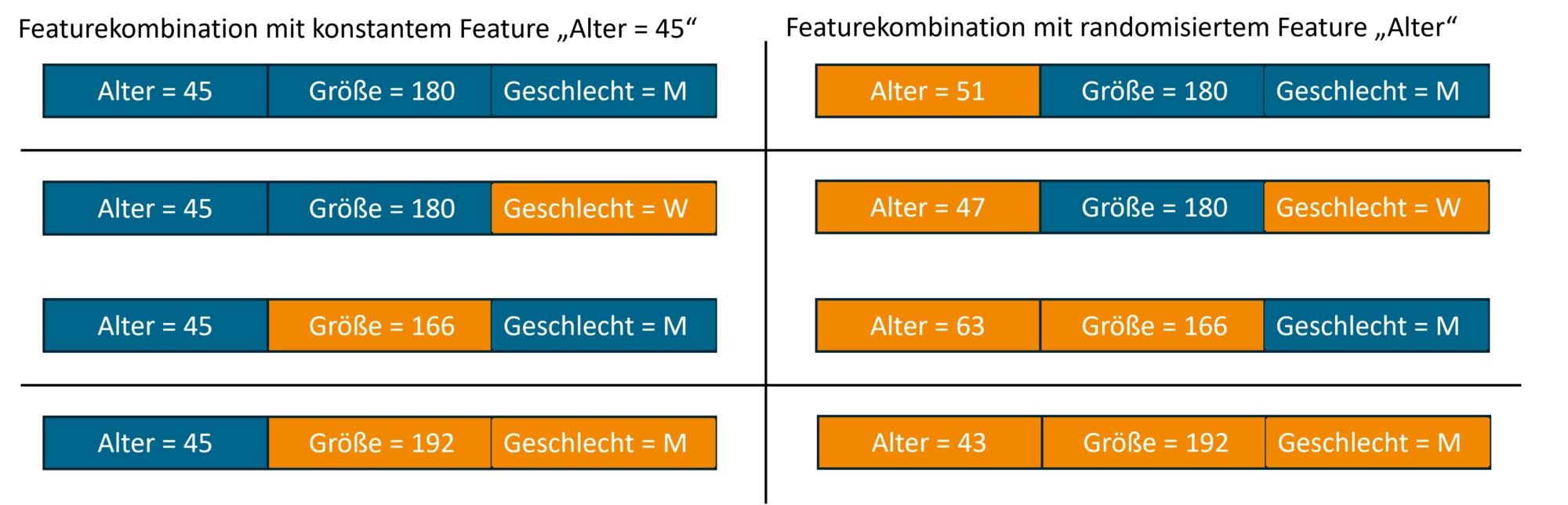
Abbildung 1: Gezeigt sind alle möglichen Kombinationen bei einem Beispiel von drei Features. Hier liegt der Fokus auf dem Feature „Alter“ indem untersucht wird, inwiefern sich dieses Merkmal auf die Vorhersagen des Modells auswirkt. Die linke Seite beinhaltet alle Featurekombinationen in denen der Wert für „Alter“ konstant bleibt. Hingegen beinhaltet die rechte Seite die restlichen Kombinationen, bei denen der Wert für „Alter“ randomisiert wurde. In der obersten Zeile sehen wir auf der linken Seite eine Kombination mit allen drei Features. Rechts sehen wir die gleiche Kombination nur dass der Wert für das Feature „Alter“ randomisiert wurde. In der nächsten Zeile sehen wir das Beispiel einer Menge an Features, die die konstanten Werte von „Alter“ und „Größe“ beinhaltet. Das Merkmal „Geschlecht“ wurde mit einem zufälligen Wert versehen (links). Analog sehen wir auf der rechten Seite die gleiche Menge an Features, wobei „Alter“ und „Geschlecht“ mit einem zufälligen Wert aufgefüllt wurden. Analoges gilt für die letzten beiden Zeilen. Features mit unveränderten Werten sind blau gefärbt. Orangefarbene Merkmale werden durch zufällige Werte aus dem Hintergrunddatensatz aufgefüllt und besitzen somit keine Wichtigkeit für die Vorhersage.

SHAP kann sowohl globale als auch lokale Erklärungen liefern. Beim globalen Ansatz werden zusammenfassende Erklärungen in Form von Verteilungen der SHAP-Werte aus mehreren Einträgen des Datensatzes erzeugt. Hierdurch kann man verstehen, inwiefern sich einzelne Features auf das Modellverhalten auswirken und welche Merkmale besonders einflussreich sind. Im Gegensatz dazu bezieht sich eine lokale Erklärung immer nur auf eine einzelne Instanz und erklärt die Entscheidung des Modells in einem konkreten Fall.

Vorteilhaft für den Nutzer ist zudem die Erstellung von anschaulichen Grafiken, die die globalen und lokalen Erklärungen verständlich abbilden und viel Information übersichtlich darstellen. Allerdings weisen die SHAP-Plot-Funktionen uneinheitliche Parameter-Schnittstellen auf, die das Verständnis der technischen Anwendung erschweren können. Später im Text werden wir nochmals auf zwei beispielhafte SHAP-Plots näher eingehen. Dies sind zum einen der Dot-Plot, der eine globale Erklärung darstellt und zum anderen der Waterfall-Plot, der beispielhaft für eine lokale Erklärung steht.

Ebenfalls integriert SHAP andere XAI-Methoden, u.a. LIME¹ (Local Interpretable Model-agnostic Explanations), welches ebenso eine sehr bekannte Technik aus dem Feld der XAI ist.

SHAP: Worauf es zu achten gilt

Eine besonderere Herausforderung von SHAP liegt in der langen Rechenzeit, die abhängig von der Komplexität der Daten ist. Die Anzahl an allen möglichen Kombinationen steigt mit der Anzahl an Merkmalen im Datensatz exponentiell an. Diese Problematik haben die Entwickler ein Stück weit entschärft, indem sie Algorithmen entwickelt haben, die für spezifische Modelle laufzeit-technisch optimiert sind. Ein bestimmter Algorithmus namens KernelSHAP ist hingegen modell-agnostisch und approximiert die Shapley-Werte, um eine Beschleunigung zu ermöglichen. Zudem ist es auch möglich, die Rechenlast auf mehreren CPU-Kernen zu verteilen, also die SHAP-Werte auf parallelisierte Weise zu berechnen. Dies hat zur Folge, dass die Rechenzeit verkürzt werden kann. Allerdings lohnt sich die Parallelisierung erst ab einer Datenmenge von mehreren Tausend Instanzen. Außerdem geht SHAP im Allgemeinen von der Unabhängigkeit der einzelnen Features aus. In der Realität weisen aber die Features gewisse Zusammenhänge auf. Die Annahme, dass Features unabhängig voneinander sind, kann als Nachteil der Methode angesehen werden.

Da SHAP in vielen unterschiedlichen Problemen einsetzbar ist und diverse Möglichkeiten bietet, ein Machine Learning-Modell und seine Entscheidungsfindung nachzuvollziehen, wollen wir uns im nächsten Abschnitt zwei beispielhafte SHAP-Plots in einem konkreten Fall der Anomalieerkennung näher anschauen.

KI-gemachte Entscheidungen als Mensch nachvollziehen

Es gibt mehrere Arten von globalen Plots, mit denen man sich einen generellen Überblick über einen Teil oder den gesamten Datensatz verschaffen kann (globale Erklärung). Im Folgenden wird beispielhaft ein globaler Dot-Plot gezeigt. Bei dem folgenden Problem handelt es sich um eine binäre Klassifikation von Netzwerkverkehrsdaten. Hierbei gibt es zwei Klassen: Nicht-Anomalie (Klasse 0) und Anomalie (Klasse 1).

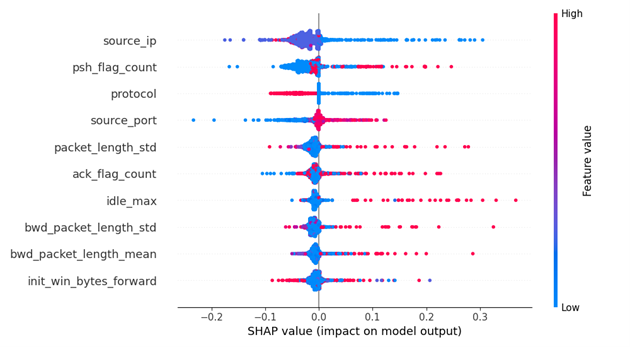
Abbildung 2: Die Features mit den stärksten Einflüssen auf das Modellverhalten können mittels eines globalen Dot-Plots visualisiert werden. Zudem stellt der Dot-Plot die Zusammenhänge zwischen den Ausprägungen der Features und des Modellverhaltens dar.

Die Features des Datensatzes werden auf der y-Achse nach ihrer Einflussstärke auf die Vorhersage angeordnet. Die wichtigsten Features befinden sich ganz oben. Je weiter oben sich eine Variable befindet, umso höher ist der entsprechende (absolute) SHAP-Wert bzw., umso stärker ist der Einfluss dieser Variable auf die Vorhersage.

Auf der x-Achse ist der Bereich, in dem sich die berechneten SHAP-Werte befinden, aufgetragen. Die SHAP-Werte spiegeln die Einflussstärke der Variablen auf die Vorhersage der Instanzen wider. Für jede Beobachtung wird je Feature ein einzelner Punkt eingezeichnet.

Im Dot-Plot wird ersichtlich, dass niedrige Werte des Features source_ip (in Blau) hohe SHAP-Werte aufweisen. Das bedeutet, dass geringe Werte von source_ip für eine anomale Instanz sprechen. Im Gegensatz dazu scheinen hohe (rot) und mäßig hohe Werte (lila) eher typisch für regulären Verkehr zu sein. Eine deutlichere Aufteilung der Werte ist bei dem Merkmal protocol erkennbar. Bei source_port sieht man eine eher gegenteilige Tendenz, wobei hohe Werte auf eine anomale Betrachtung hinweisen.

Der lokale Waterfall-Plot bildet die Erklärung einer einzelnen Vorhersage ab, sodass man die Möglichkeit bekommt, diese näher zu analysieren. Genau wie beim vorhin erwähnten Dot-Plot, werden die Variablen ebenso nach ihrer Wichtigkeit angeordnet.

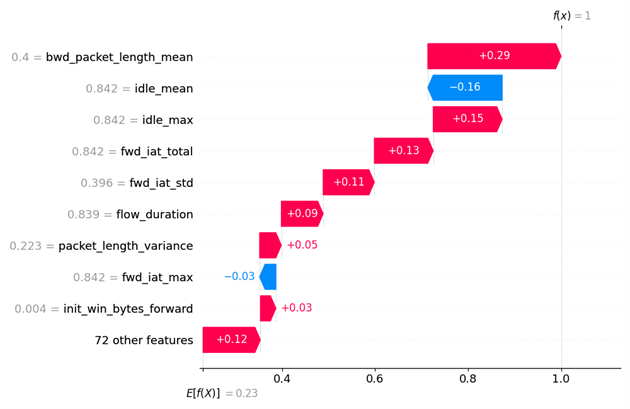
Abbildung 3: Der Waterfall-Plot hilft dabei zu verstehen, inwiefern sich eine Vorhersage von einer einzelnen Beobachtung sich vom Erwartungswert unterscheidet. In dieser Plotform kann man genau sehen welches Feature mit welcher Ausprägung die Vorhersage in welche Richtung verschiebt.

Gestartet wird bei dem Erwartungswert E[f(x)]. Das ist der Durchschnittswert für alle Vorhersagen auf dem zugrundeliegenden Hintergrund-Datensatz. Auf diesen Mittelwert werden positive und negative SHAP-Werte addiert. Features mit einem positiven Beitrag zur Vorhersage werden mit einem roten Balken dargestellt. Im Gegensatz dazu symbolisieren blaue Balken die Features, die einen negativen Einfluss auf die Vorhersage haben. Die grauen Zahlen links neben den Variablennamen sind die zugrundeliegenden Featurewerte aus dem Datensatz. Anhand eines Waterfall-Plots wird ersichtlich, inwiefern sich die einzelnen Variablen auf die Vorhersage einer konkreten Instanz auswirken.

Bei dieser Instanz hat das Machine Learning-Modell eine Anomalie (Klasse 1) vorhergesagt. Feature bwd_packet_length_mean übt mit einem SHAP-Wert von 0,29 den stärksten Einfluss auf diese Vorhersage aus (in Rot). Das nächsteinflussreichste Feature ist idle_mean mit einem Wert von –0,16 (in Blau). Dieses Feature spricht gegen eine Anomalie. Allgemein lässt sich feststellen, dass die meisten Merkmale die Vorhersage dieser Instanz in Richtung Anomalie drücken.

Fazit

SHAP genießt im wissenschaftlichen Bereich der XAI viel Aufmerksamkeit und bietet einen praktikablen Ansatz für die unterschiedlichsten industriellen Kontexte. Aus heutiger Sicht ist das Gebiet der XAI aber noch recht klein. Dennoch ist davon auszugehen, dass im Zuge der weiteren Forschung SHAP von zukünftigem Input seitens der XAI profitieren und sich somit selbst stetig weiterentwickeln und verbessern wird. Die SHAP-Bibliothek in Python wird regelmäßig aktualisiert und ausführlich dokumentiert².

Es ist davon auszugehen, dass SHAP in der Zukunft weiterhin eine wichtige Rolle im Feld der XAI spielen wird.

1. Im Gegensatz zu LIME und weiteren Ansätzen, bietet SHAP eine solide Grundlage aus dem Bereich der kooperativen Spieltheorie. Darüber hinaus garantiert SHAP als einzige Feature Attributions-Methode wünschenswerte mathematische Eigenschaften. Die erste Eigenschaft ist die lokale Genauigkeit. Wenn ein vereinfachter Input dem ursprünglichen Input ähnelt, so muss die Vorhersage einer vereinfachten Instanz mithilfe des Erklärermodells mit der Vorhersage des ursprünglichen Inputs mittels des tatsächlichen Modells übereinstimmen. Zweitens, falls ein Feature nicht für die Prognose einer Instanz herangezogen wurde, dann hat dieses fehlende Feature keinen Einfluss auf die Prädiktion. Der Einfluss ist also gleich Null. Zu guter Letzt gibt es die Konsistenz. Wenn sich das Modell insofern verändert, dass der Beitrag eines Merkmals sich erhöht hat oder unverändert geblieben ist, dann steigt der dazugehörige SHAP-Wert entsprechend oder bleibt gleich. Genauere mathematische Ausführungen lassen sich im SHAP-Paper nachlesen ([1705.07874] A Unified Approach to Interpreting Model Predictions (arxiv.org)). ↩︎
2. Genaueres ist in diesem GitHub-Repository zu sehen: GitHub – shap/shap: A game theoretic approach to explain the output of any machine learning model.^* ↩︎