Alles hat einen Anfang und ein Ende. Aber wann fängt es an? Und wann hört es auf? Mit diesen Fragen stößt man auf den Kern der Survival-Analyse. Survival-Modelle schätzen, wieviel Zeit vergeht, bis ein bestimmtes Ereignis – ob positiv oder negativ – eintritt. Ursprünglich bestand das Ziel darin, den voraussichtlichen Todeszeitpunkt von Personen zu schätzen. Heute hat sich das Anwendungsfeld längst auf die verschiedensten Disziplinen und Gebiete ausgedehnt.
Survival-Analyse: Eine Grundidee – viele Anwendungsbereiche
Grundlage für den Einsatz von Survival-Analysen ist das Vorliegen von Mortalität, welche das sukzessive Ausscheiden von Messobjekten aus der statistischen Erfassung beschreibt. Die Grundidee von Ereigniszeitanalysen, wie Survival-Analysen auch genannt werden, wurde bereits in vielen Anwendungsbereichen adaptiert:
- Industriekonzerne ermitteln auf Basis der Erkenntnisse aus Ereigniszeitanalysen, wann ein Maschinenausfall droht um ihre Instandhaltungsprozesse daraufhin anzupassen und kostenintensive Maschinenausfälle zu vermeiden. In die Bestimmung der Ausfallrate fließen neben Zustandsdaten von Maschinenkomponenten auch Informationen aus Drittsystemen (CRM-Systeme etc.) mit ein.
- Customer-Relationship und Churn-Management Systeme können mit demografischen Informationen der Kunden und relevanten Marktinformationen für Vorhersagemöglichkeiten erweitert werden. So lässt sich ermitteln wann ein Neukunde bereit ist einen Vertrag abzuschließen, oder ein Bestandskunde droht abzuwandern. Proaktive Gegenmaßnahmen wie Rabatte, Prämien oder Boni können eingeleitet werden.
- In der Sozialforschung werden Aussagen zu beginnenden oder endeten Lebensphasen anhand von Daten aus sozialen Netzwerken getroffen. Alter, Beruf, Herkunft oder Schulabschluss der Partner sind Indikatoren, anhand derer beispielsweise die Überlebensdauer einer Beziehung bis zu einer möglichen Trennung prognostiziert wird.
Survival-Analysen geben entscheidende Einblicke in Prozessabläufe und erhöhen als belastbare Entscheidungsgrundlage die Handlungsfähigkeit. Im ökonomischen Umfeld werden Kosten gesenkt und die Effizienz von Produktion und Vertrieb gesteigert.
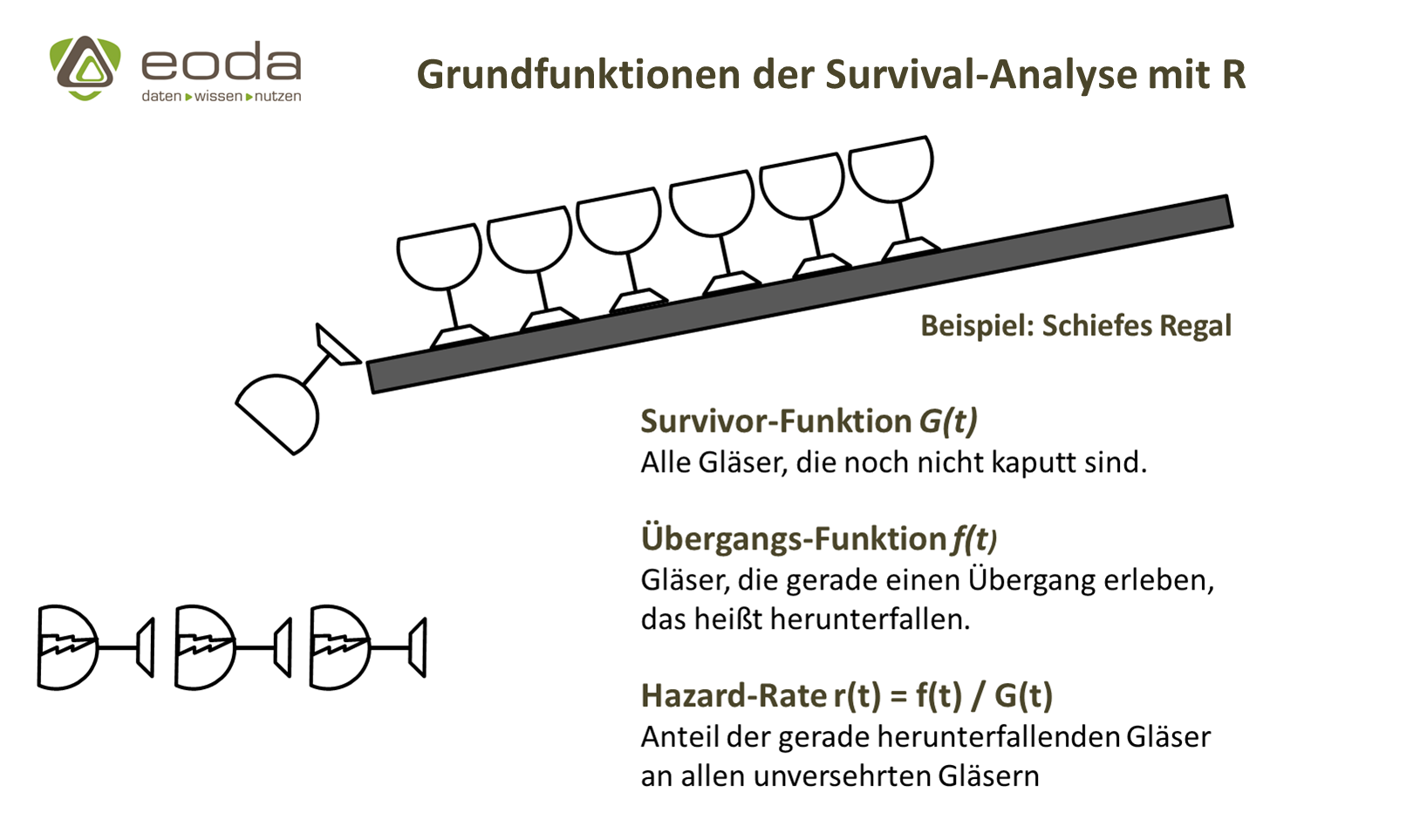
Survivor-Function und Hazard-Rate als Grundfunktionen
Methodisch grenzt die Survival-Analyse zwei wichtige Grundfunktionen voneinander ab: Survivor-Funktion und Hazard-Rate. Die Survivor-Funktion beschreibt den Anteil der Fälle, bei denen das untersuchte Ereignis noch nicht eingetreten ist. Die Hazard-Rate hingegen steht für das unmittelbare Risiko des Eintretens des Ereignisses für einen bestimmten Fall.
survival: Das Erweiterungspaket für die Survival-Analyse mit R
Methoden für diese und weitere Verfahren im Rahmen der Survival-Analyse wie den Kaplan-Meier-Schätzer für die Wahrscheinlichkeitsschätzung und die Cox Regression zur Modellierung von Überlebenszeiten vereint das Erweiterungspaket survival der Open Source Statistiksoftware R. R wartet für Survival-Analysen ein breites Methodenset für individuelle Aufgabenstellungen auf. Global Leader wie John Deere, Google oder Facebook nutzen R bereits für die Durchführung ihrer prädiktiven Analysen.
Neuer Kurs zum Thema Survival-Analyse im Rahmen der eoda Data Science Trainings
Im Rahmen der Data Science Trainins veranstaltet eoda am 12. November den Kurs „Zeitreihenanalyse mit R II“. Während des Kurses wird sowohl die Grundidee der Survival-Analyse als auch deren praktische Umsetzung mit R vermittelt. Die Verfahren werden auf Beispieldaten angewendet und durch praktische Übungsphasen vertieft. Mit dem Kurs werden die Teilnehmer in die Lage versetzt, eigene Analysekontexte mit Hilfe folgender Verfahren zu bearbeiten:
- Grundlegende Verfahren der Survival-Analyse mit R
- Kaplan-Meier-Schätzer
- Cox-Proportional-Hazards-Modell
- Zeitveränderliche Variablen & Episoden-Splitting
- Cox Regression
Als Ergänzung zu diesem Kurs versteht sich der Kurs „Zeitreihenanalyse mit R I“, der am 10. und 11. November stattfindet und eine optimale Wissensgrundlage für den zweiten Teil der Zeitreihenanalyse mit R liefert – welcher den Teilnehmern dann Aufschluss über den Zeitpunkt von Anfang und Ende liefert.
Hier entlang.