Seit dem 22. Dezember läuft unser Gewinnspiel anlässlich der nahenden 10.000 R-Pakete Marke. Viele interessante Lösungsvorschläge sind seitdem bei uns eingegangen, zum Teil sogar mit detaillierten Prognosemodellen in Form von R-Code. Natürlich wollten auch wir eine Vorhersage treffen und haben zwei unterschiedliche Herangehensweisen mit R getestet, welche wir in diesem Blogartikel vorstellen.
Bei der ersten Methode haben wir die Pakete-Liste nach Erscheinungsdatum auf CRAN als Datengrundlage herangezogen. Da diese Liste nicht nur neu erschienene Pakete sondern auch Aktualisierungen erfasst, wurde sie mit den Informationen aus dem Pakete-Archiv abgeglichen und um die Pakete bereinigt, die bereits vorhanden waren und lediglich aktualisiert wurden.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
# Bereinigung und Aufbereitung der Daten.
df_archive < – as.data.frame(cran_archive)
df_cran <– as.data.frame(cran_by_date)
df_archive <– df_archive[–1:–2, ]
df_archive <– df_archive[, c(–1, –4, –5)]
df_cran <– df_cran[, 1:2]
df_cran <– data.frame(date = df_cran[, 1], package = df_cran[, 2])
df_archive <– data.frame(date = df_archive[, 2], package = df_archive[, 1])
df_cran$date <– as.Date(df_cran$date)
df_archive$date <– as.character(df_archive$date)
df_archive$package <– gsub(„/“, „“, df_archive$package)
df_archive$date <– gsub(“ .*“, „“, df_archive$date)
df <– rbind(df_cran, df_archive)
# Löschen aller Pakete aus dem cran Datensatz die auch im Archiv vorhanden
# sind.
library(dplyr)
df_new <– df %>% group_by(package) %>% filter(n() == 1)
|
Mithilfe des forecast Pakets wurde eine Vorhersage für die nächsten 30 Tage getroffen.
|
1
2
3
4
5
6
7
|
# Auswahl des Beobachtungszeitraums. Hier 30 Tage.
df_tail < – tail(data.frame(table(df_new$date)), 30)
df_tail$cum <– cumsum(df_tail$Freq)
# Anwenden von forecast mit Vorhersage für die nächsten 30 Tage.
df_forecast <– forecast(df_tail$cum, 30)
summary(df_forecast)
|
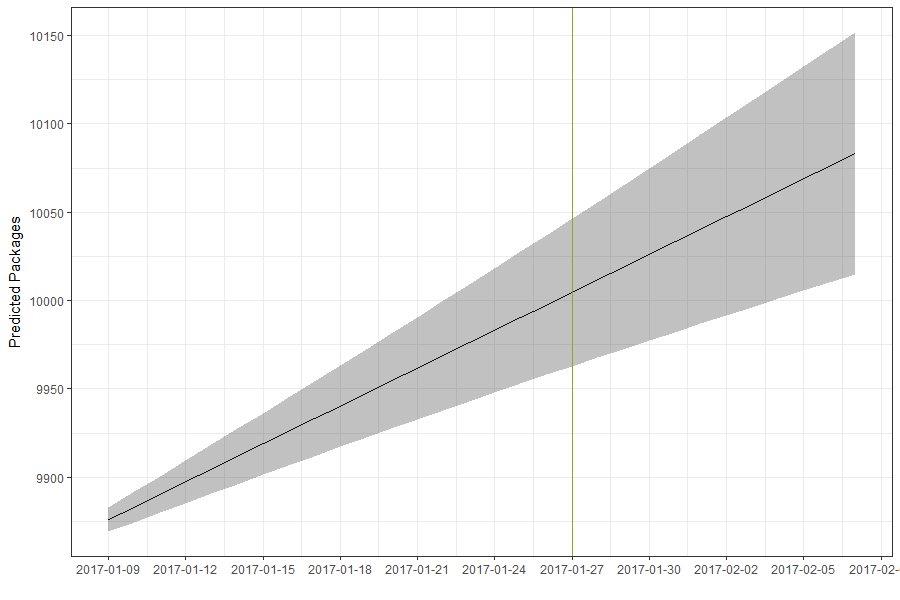
Anschließend wurde die Anzahl der Pakete bis zur 10.000 Marke ermittelt und das Ergebnis als Plot dargestellt.
|
1
2
3
4
5
6
|
# Anzahl der Pakete bis zur 10000 Pakete Marke für den Teildatensatz. In
# diesem Fall 368.
10000 – (length(df_cran$date) – max(df_tail$cum))
aim_packages < – 10000 – (length(df_cran$date) – max(df_tail$cum)) # Das Ergebnis als Plot mit 10000 Pakete Schwelle, minimum Grenze, # Mittelwert und Maximale Anzahl an Tagen. plot(df_forecast) abline(a = aim_packages, b = 0, lty = 1, col = „black“, lwd = 3) lines(c(min(which(df_forecast$lower[, 2] > aim_packages)) – 1 + 30, min(which(df_forecast$lower[, 2] > aim_packages)) – 1 + 30), c(0, 500))
lines(c(min(which(df_forecast$upper[, 2] > aim_packages)) – 1 + 30, min(which(df_forecast$upper[, 2] > aim_packages)) – 1 + 30), c(0, 500))
lines(c(min(which(df_forecast$mean > aim_packages)) – 1 + 30, min(which(df_forecast$mean > aim_packages)) – 1 + 30), c(0, 500))
|
Hieraus ergab sich eine Dauer von 25 Tagen vom Berechnungszeitpunkt (02.01.) bis zur Erreichung des 10.000 Pakets und somit der 27.01.2017 als Erscheinungsdatum.
|
1
2
3
|
# Der Tag an dem die 368, also 10000, Pakete erreicht werden.
df_forecast$mean[min(which(df_forecast$mean > aim_packages)) – 1]
# Stichtag 2.1. + 25 Tage = 27.1.2017
|
In einer zweiten Methode haben wir die Daten unseres eigens für das Gewinnspiel entwickelten Twitter-Bots als Datengrundlage genutzt und mithilfe einer linearen Regression die Dauer bis zur Veröffentlichung des 10.000 Pakets errechnet. Auch mit diesem Vorgehen erhielten wir als Lösung den 27.01.2017.
|
1
2
3
4
5
6
7
|
# Mit den Daten vom Twitter-Bot und linearer Regression
df_twitter < – data.frame(day = c(0, 5, 6, 7, 8, 9, 10, 11),
packages = c(9763, 9787, 9799, 9808, 9814, 9823, 9828, 9832))
lm1 <– lm(packages ~ day, df_twitter)
# Wieder 2.1. + 25 Tage = 27.1.2017
(10000 – max(df_twitter$packages)) / coefficients(lm1)[2] + 2
|
Ob wir mit diesem Datum richtig liegen, werden wir in den nächsten Tagen erfahren, denn aktuell trennen uns nur noch knapp 30 Pakete von der 10.000 Marke. Doch bis dahin wünschen wir weiterhin allen Teilnehmern viel Erfolg