Die lineare Regression gehört zu den am häufigsten verwendeten Verfahren in der statistischen Datenanalyse. Sie findet Verwendung in der Mustererkennung und zur Prognose und hat eine lange Tradition in Forschung und Lehre. Sie ist auch für statistische Laien verständlich, rechnerisch wenig aufwendig und vielseitig einsetzbar. Ziel der Regression ist es, den kausalen Zusammenhang einer abhängigen Variable durch ein Set erklärender Variablen zu analysieren.
Einsatzmöglichkeiten der Regressionsanalyse
In der Praxis könnte mit der linearen Regressionsanalyse zum Beispiel versucht werden, den Einfluss einzelner Aspekte der Kundenzufriedenheit auf die Gesamtzufriedenheit zu bestimmen.
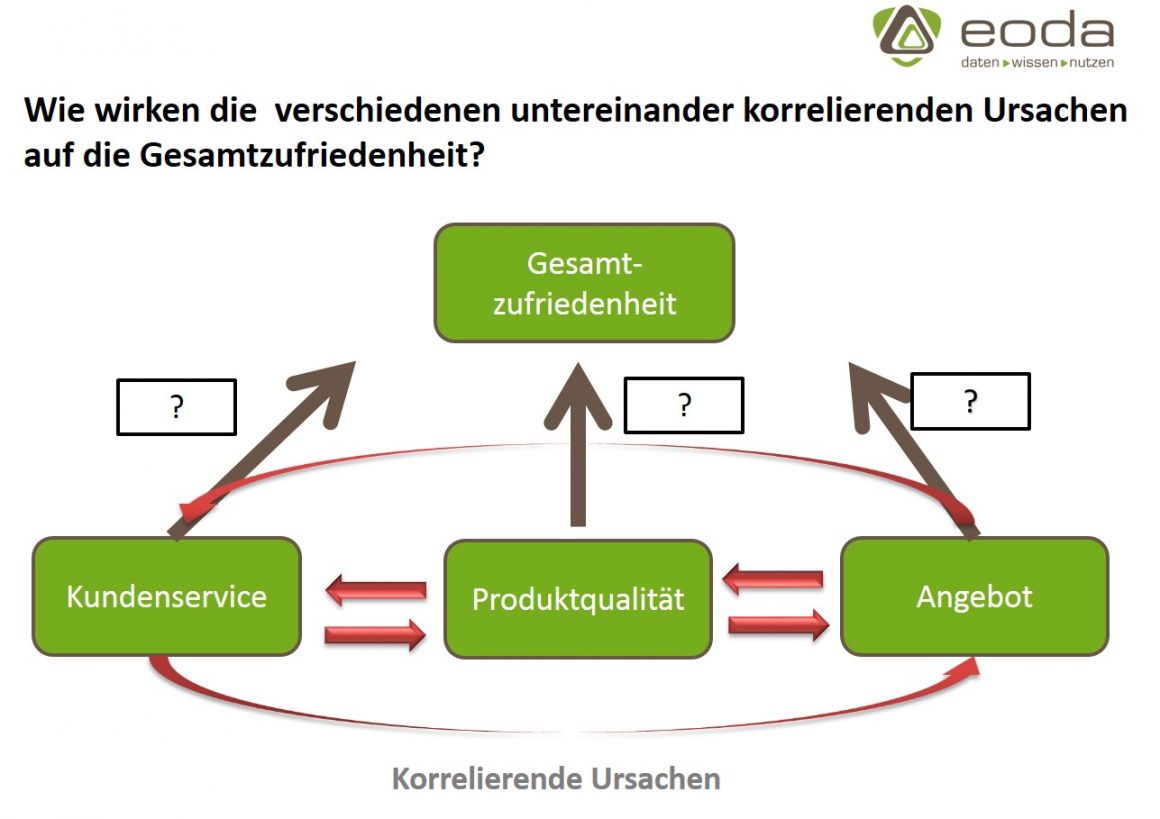
Eine typische Interpretation der Ergebnisse einer linearen Regression lautet: Wenn sich die Zufriedenheit mit dem Service um einen Punkt erhöht, dann erhöht sich die Gesamtzufriedenheit um 0,4 Punkte. Darüber hinaus kann die Regression erklären, welche Teilzufriedenheiten den größten Einfluss auf die Gesamtzufriedenheit haben. Maßnahmen zur Verbesserung der Gesamtzufriedenheit können sich dann zunächst auf die wichtigsten Teilaspekte fokussieren. Schließlich können die Ergebnisse der Regressionsanalyse zur Prognose verwendet werden. Sind im Beispiel die Teilzufriedenheiten bekannt, so kann die Gesamtzufriedenheit geschätzt werden, auch wenn diese selbst nicht bekannt ist. Diese Methode ist vor allem für Problemstellungen interessant, die sich auf die Zukunft beziehen: Der Umsatz im nächsten Quartal, die Anzahl der Bestellungen eines Artikels, die Ausfallwahrscheinlichkeit eines Bauteils etc. Je besser das Regressionsmodell den tatsächlichen Verhältnissen entspricht, desto genauer ist die Schätzung.
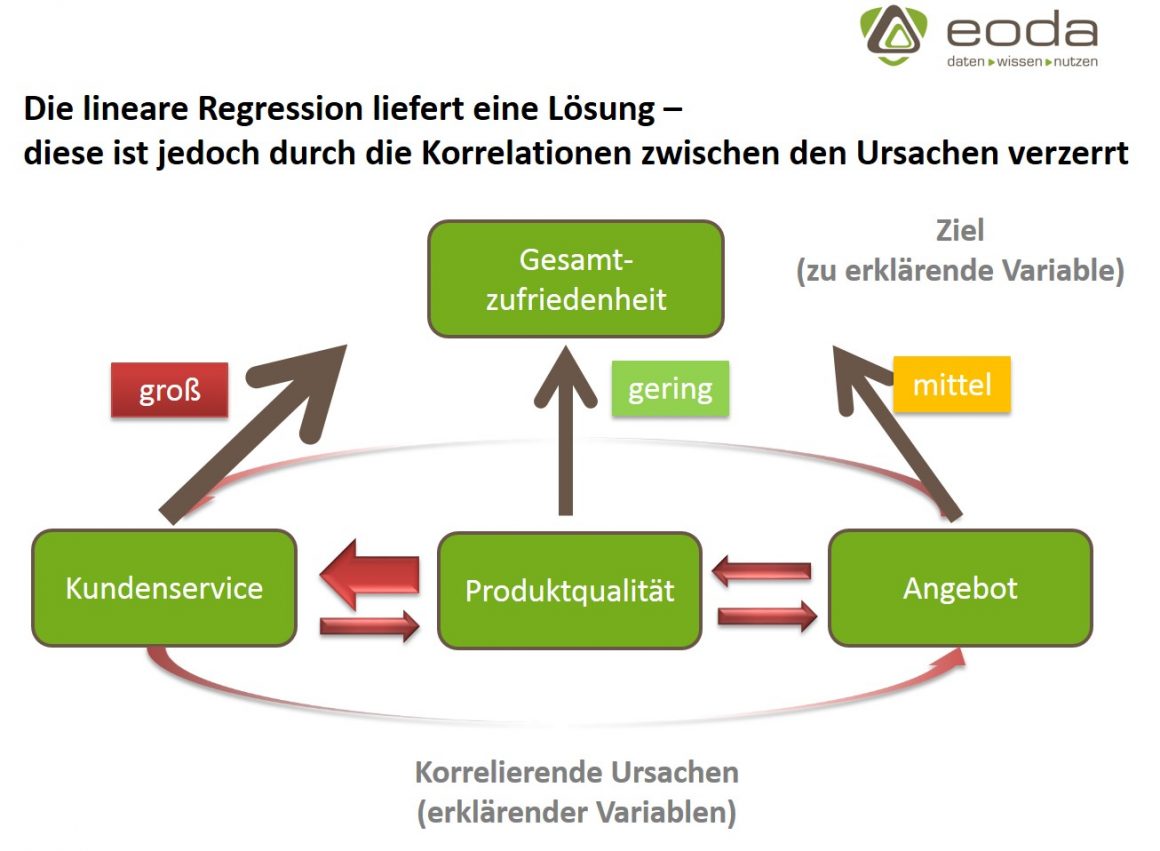
Voraussetzungen der Regressionsanalyse
Nicht allen Anwendern ist jedoch bekannt, dass die Regressionsanalyse hohe Anforderungen an das Datenniveau der erklärenden Variablen stellt. Eine dieser Voraussetzungen ist, dass die erklärenden Variablen voneinander unabhängig sein sollen. Diese Bedingung ist in der Praxis häufig nicht erfüllt. Wenn wie im Beispiel die Gesamtzufriedenheit der Kunden anhand einer Reihe von Teilzufriedenheiten (mit dem Kundenservice, der Produktqualität, der Übersichtlichkeit des Angebots etc.) erklärt werden soll, sind diese Teilzufriedenheiten in der Regel nicht voneinander unabhängig.
Beispielsweise wird der Kundenservice im Falle eines hochwertigen Produktes weniger in Anspruch genommen. Umgekehrt ist der Kundenservice im Falle eines minderwertigen Produktes überlastet und somit schlechter erreichbar und wirkt weniger freundlich und kompetent. Die Zufriedenheit mit der Produktqualität korreliert mit der Servicezufriendenheit. Beide Teilzufriedenheiten wirken kausal auf die Gesamtzufriedenheit. Die Effekte der jeweiligen Teilzufriedenheiten lassen sich analytisch jedoch nicht voneinander trennen.
Korrelierende erklärende Variablen
Die Schätzung der Regressionskoeffizienten und der Modellgüte (r²) wird im Fall von Korrelationen zwischen den erklärenden Variablen möglicherweise ungenau. Darüber hinaus kann unter diesen Umständen ein Phänomen auftreten, dass unter dem Namen „Simpson Paradox“ bekannt ist. Ein Effekt des Simpson-Paradoxons besteht darin, dass Koeffizienten, die in Wahrheit positiv sind, im Modell als negativ ausgewiesen werden. Das bedeutet z.B. dass ein kausaler Zusammenhang, der in der Realität in der Form „je mehr desto mehr“ vorliegt, auf Grund der nicht gegebenen Unabhängigkeit der erklärenden Variablen als „je mehr desto weniger“ ausgewiesen wird. Das Modell wird ungenau, schlimmstenfalls sogar irreführend. Die Ergebnisse der Analyse können nicht vorbehaltslos interpretiert werden.
Was ist zu tun? In der Praxis wird die Voraussetzung der Unabhängigkeit der erklärenden Variablen häufig aufgeweicht. Statt der Unabhängigkeit wird nur noch „keine starke Abhängigkeit“ verlangt. Verstoßen erklärende Variablenpaare gegen die abgeschwächte Unabhängigkeitsbedingung, wird eine der Variablen aus dem Modell entfernt. Dies ist jedoch aus inhaltlichen Gründen oft nicht sinnvoll.
Die Shapley Value Regression
Eine bessere Alternative bietet ein Ansatz aus der Spieltheorie, die nach dem diesjährigen Nobelpreisträger Lloyd Shapley benannte Shapley Value Regression. Der Grundgedanke des Shapley Value ist, den Beitrag einzelner Spieler zum Gesamtergebnis eines kooperativen Spiels zu ermitteln. Auf die Regressionsanalyse angewendet werden die erklärenden Variablen als Spieler aufgefasst, die zum Gesamtergebnis – der Modellgüte – beitragen. Die Shapley Value Regression ist in der Lage sowohl den Beitrag der erklärenden Variablen als auch die Modellgüte robust zu schätzen, wenn die erklärenden Variablen korrelieren.
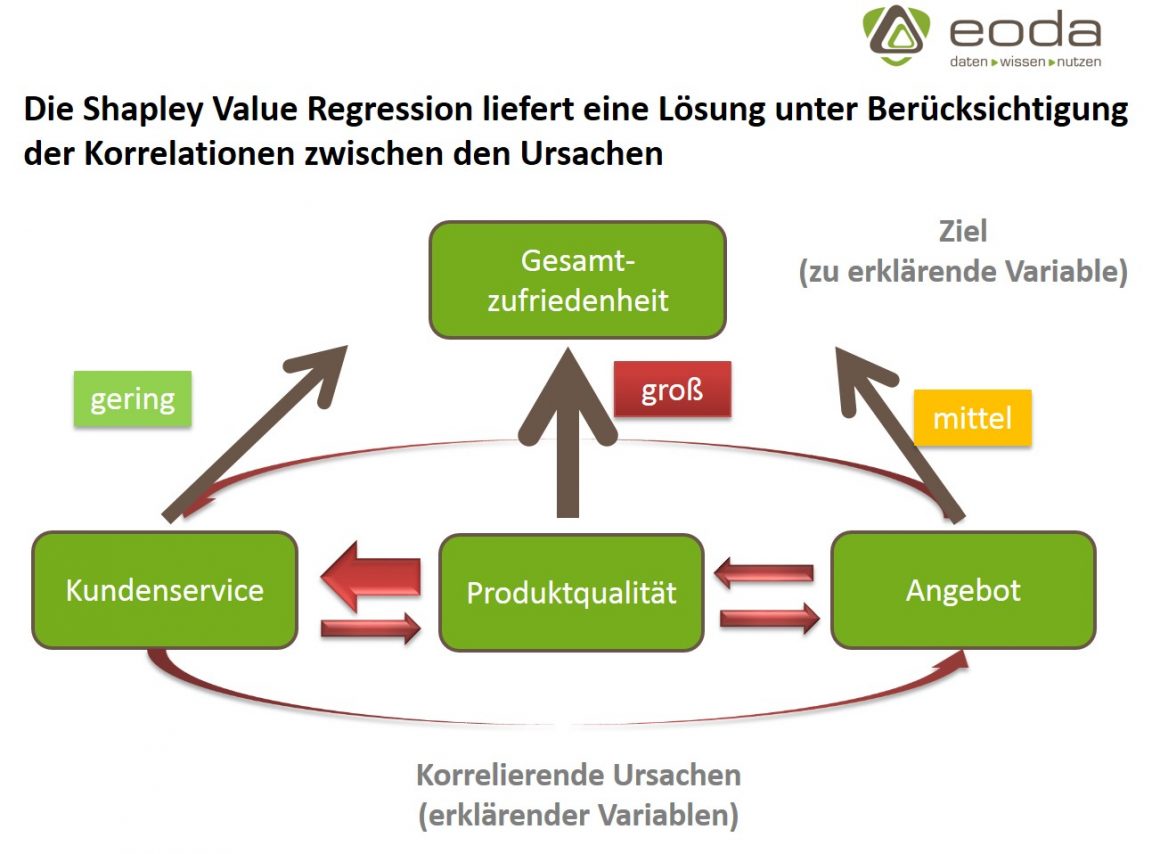
Hier entlang.